INTEGRAL
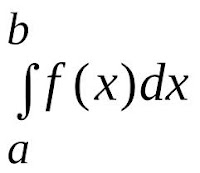
Integral adalah kebalikan dari diferensial. Apabila fungsi F(X) merupakan integral (anti derivative) function dari fungsi f(x), maka : F(x) disebut sebagai primitive function f(x) merupakan derivative/turunan dari F(x) Jadi, integral mencari fungsi asal dari fungsi f(x). Tetapi, diferensiasi mencari turunan dari F(x). Diferensiasi dari F(x) menghasilkan fungsi yang unik (a unique derivative function) f(x). Sebaliknya, integral dari f(x) menghasilkan banyak tak terbatas bentuk fungsi (indefinite number of possible parents) F(x). Notasi : ∫ adalah tanda/lambang integral f(x) adalah fungsi yang akan diintegralkan dx tanda untuk melakukan diferensiasi terhadap x ∫ f(x)dx sebagai notasi diferensiasi dari the primitive function / F(x). a dan b adalah batas integralnya. Dimana “c” adalah suatu angka yang bersifat bebas yang...

