INTEGRAL
Integral adalah kebalikan dari diferensial. Apabila fungsi F(X) merupakan integral (anti derivative) function dari fungsi f(x), maka :
- F(x) disebut sebagai primitive function
- f(x) merupakan derivative/turunan dari F(x)
Jadi, integral mencari fungsi asal dari fungsi f(x). Tetapi, diferensiasi mencari turunan dari F(x). Diferensiasi dari F(x) menghasilkan fungsi yang unik (a unique derivative function) f(x).
Sebaliknya, integral dari f(x) menghasilkan banyak tak terbatas bentuk fungsi (indefinite number of possible parents) F(x).
Notasi :
- ∫ adalah tanda/lambang integral
- f(x) adalah fungsi yang akan diintegralkan
- dx tanda untuk melakukan diferensiasi terhadap x
- ∫ f(x)dx sebagai notasi diferensiasi dari the primitive function / F(x).
- a dan b adalah batas integralnya.
Dimana “c” adalah suatu angka yang bersifat bebas yang berfungsi sebagai indikasi banyaknya fungsi primitif yang bisa dihasilkan.
- Integral ∫ f(x)dx disebut the indefinite integral of f(x) karena tidak mempunyai batasan angka tertentu.
- Integral ₐ∫ᵇ f(x)dx disebut definite integral karena mempunyai batasan angka tertentu dari angka sebesar a ke b
RULE 1

“n” sebagai pangkat dari x , dimana n tidak boleh bernilai -1. Karena nantinya pembaginya -1 + 1 = 0, Bilangan berapa pun jika dibagi 0 hasilnya tak terdefinisi/ tak hingga.
Contoh soal:
RULE 2

Integral Exponensial adalah fungsi yang dinotasikan dalam bentuk e pangkat x.
Contoh soal:
RULE 3

Contoh soal:
RULE 4

Contoh soal:
RULE 5

Contoh soal :
RULE 6

Teknik perhitungan integral pada rule ini:
1. Memilih fungsi u : g(x) sehingga ∫f (g(x)) g'(x) dx dapat diubah menjadi ∫f (u) du.
2. Tentukan fungsi integral umum = f (u) yang bersifat f’ (du) : f (u).
1. Memilih fungsi u : g(x) sehingga ∫f (g(x)) g'(x) dx dapat diubah menjadi ∫f (u) du.
2. Tentukan fungsi integral umum = f (u) yang bersifat f’ (du) : f (u).
Contoh soal:
RULE 7

Contoh soal:
RULE 8

7. ∫ cot x cosec x dx = -cosec x + c
Sifat-sifat :
 Contoh soal:
Contoh soal: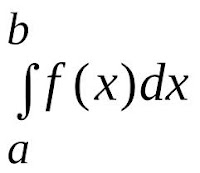










Komentar
Posting Komentar