TURUNAN FUNGSI
Turunan Fungsi (lebih dari 1 variabel)
TURUNAN PARSIAL
Turunan Fungsi dua Variabel
Turunan Parsial.
Diketahui z = f(x,y) fungsi dengan dua variabel independen x dan y. Karena x dan y independen maka :
(i). x berubah-ubah sedangkan y tertentu.
(ii). y berubah-ubah sedangkan x tertentu.
Definisi
i) Turunan parsial terhadap variabel x
Jika x berubah-ubah dan y tertentu maka z merupakan fungsi x, Turunan parsial z = f(x,y) terhadap x sbb :
ii) Turunan parsial terhadap variabel y
Jika y berubah-ubah dan x tertentu maka z merupakan fungsi
y, Turunan parsial z = f(x,y) terhadap y sbb :

a. Fungsi dua peubah atau lebih
Fungsi dua peubah atau lebih dapat ditulis dalam bentuk eksplisit atau implisit. Jika fungsi dua peubah dinyatakan dalam bentuk eksplisit, maka secara umum ditulis dalam bentuk z = F(x,y). Sebaliknya jika fungsi dituliskan dalam bentuk implisit, secara umum ditulis dalam bentuk F(x,y,z) = 0.
Contoh:
1. z = 2x + y
2. xy + xz – yz = 0
Pada contoh di atas, fungsi yang ditulis dalam bentuk eksplisit adalah pada contoh 1,2, dan 3. Sedangkan contoh 4, 5, 6, dan 7 adalah fungsi yang ditulis dalam bentuk implisit. Semua fungsi dalam bentuk eksplisit dengan mudah dapat dinyatakan dalam bentuk implisit. Akan tetapi tidak semua bentuk implisit dapat dinyatakan dalam bentuk eksplisit.
Untuk menggambar fungsi dua peubah dapat dengan membuat sumbu-sumbu koordinat, yaitu sumbu x, sumbu y, dan sumbu z.
a. Turunan Parsial Fungsi Dua dan Tiga Peubah
Misal z = F(x,y) adalah fungsi dengan variable bebas x dan y. Karena x dan y variable bebas maka terdapat beberapa kemungkinan yaitu:
- y dianggap tetap, sedangkan x berubah-ubah.
- x dianggap tetap, sedangkan y berubah-ubah
- x dan y berubah bersama-sama sekaligus.
Pada kasus 1 dan 2 diatas mengakibatkan fungsinya menjadi fungsi satu peubah, sehingga fungsi tersebut dapat diturunkan dengan menggunakan definisi turunan pertama yang telah dipelajari pada kalkulus diferensial.
Definisi
Misal z = F(x,y) adalah fungsi dua peubah yang terdefinisi pada interval tertentu, turunan parsial pertama z terhadap x dan y dinotasikan dengan
Untuk memudahkan persoalan andaikan z = F(x,y) maka untuk menentukan sama artinya dengan menurunkan variabel x dan variabel y dianggap konstan dan selanjutnya y diturunkan. Demikian pula untuk menentukan sama artinya dengan menurukan variable y dan variable x dianggap konstant lalu diturunkan. Dengan cara yang sama, andaikan W = F(x,y,z) adalah fungsi tiga peubah yang terdefinisi dalam selang tertentu maka turunan parsial pertama dinyatakan dengan , dan yang secara berturut didefinisikan oleh:
Asalkan limitnya ada.
Selanjutnya turunan parsial fungsi dua peubah atau lebih dapat ditentukan turunan parsial ke n, untuk n  2 turunan parsialnya dinamakan turunan parsial tingkat tinggi.
2 turunan parsialnya dinamakan turunan parsial tingkat tinggi.
Dengan menggunakan analogi fungsi satu peubah dapat ditentukan turunan parsial tingkat 2, 3 dan seterusnya.
. Differensial Total dan Turunan Total
Misal z = F(x,y), dan fungsi tersebut dapat diturunkan terhadap variable x dan y, maka diperoleh turuna parisal terhadap x dan turunan parsial terhadap y yang secara berturut-turut dinotasikan dengan.
Turunan Parsial Fungsi Implisit
Fungsi Implisit 4 Peubah
BU dinyatakan dengan
Atau ditulis dalam bentuk
F(x,y,u,v) = 0 dan G(x,y,u,v) = 0
dengan x,y variable berpasangan dan u,v variabel berpasangan dan F(x,y,u,v) = 0 serta G(x,y,u,v) = 0 tidak dapat berdiri sendiri.
Untuk menentukan turunan parsial 4 peubah, langkah ditempuh adalah menurunkan fungsi terhadap peubah yang dimaksud.
Contoh:
Turunan fungsi aljabar merupakan fungsi lain dari suatu fungsi sebelumnya, sebagai contoh fungsi f menjadi f’ yang memiliki nilai tidak beraturan.
Pada dasarnya konsep turunan sering sekali kita pakai dalam kehidupan sehari-hari.
Baik itu di dalam ilmu matematika atau ilmu yang lainnya.
Fungsi dari turunan sendiri yang sering kita ketahui merupakan menghitung garis singgung pada suatu kurva atau fungsi dan kecepatan.
Tak hanya itu saja, konsep turunan ini juga sering dipakai dalam mencari laju pertumbuhan organisme (biologi), keuntungan marjinal (ekonomi), kepadatan kawat (fisika) serta laju pemissahan (kimia).
Pengertian
Pengertian Turunan
Turunan atau disebut juga seabagai Deriviatif merupakan suatu pengukuran kepada bagaimana fungsi berubah seiring perubahan nilai input.Secara umum, turunan akan menyatakan bagaimanakah sebuah besaran berubah akibat adanya perubahan besaran yang lainnya.
Sebagai contoj: turunan dari posisi suatu benda yang kemudian bergerak terhadap waktu merupakan kecepatan sesaat oleh objek tersebut.
Proses dalam menemukan suatu turunan disebut sebagai diferensiasi. Serta kebalikan dari suatu turunan disebut seabgai Anti Turunan.
Teorema atau pernyataan fundamental kalkulus menyebutkan bahwa antiturunan merupakan sama dengan integrasi.
Turunan dan juga integral merupakan 2 buah fungsi penting yang ada di dalam kalkulus.
- (in x)’
- (sin x)’ = cos x
- (cos x)’ = -sin x
- (tan x) = sec2 x
- y’ merupakan simbol untuk turunan pertama.
- y” merupakan simbol untuk turunan kedua.
- y”’ merupakan simbol untuk turunan ketiga.

Pengertian Turunan Fungsi
Seperti
yang telah kita sebutkan di atas, Turunan Fungsi atau yang disebut jua
sebagai diferensial merupakan suatu fungsi lain dari suatu fungsi
sebelumnya.
Contohnya fungsi f menjadi f’ yang mempunyai nilai yang tidak beraturan.
Konsep
turunan sebagai bagian utama dari materi kalkulus dipikirkan pada waktu
yang bersamaan oleh seorang Ilmuan Ahli matematika sekaligus Fisika
berkebangsaan inggris yang bernama Sir Isaac Newto (1642 – 1727). Serta
oleh seorang ahli matematika berbangsa Jerman yang bernama Gottfried
Wilhelm Leibniz (1646 – 1716).
Turunan atau
diferensial dipakai sebagai sebuah alat untuk menyelesaikan berbagai
permasalah yang dijumpai di dalam bidang geometri dan mekanika.
Konsep turunan fungsi secara universal atau menyeluruh banyak sekali dimanfaatkan di dalam berbagai bidang keilmuan.
Sebut saja dalam bidang ekonomi: yang dipakai guna menghitung berupa, biaya total atau total penerimaan.
Pada bidang biologi: dipakai untuk menghitung laju pertumbuhan organisme.
Pada bidang fisika: di pakai untuk menghitung kepadatan kawat.
Pada bidangkimia: dipakai untuk menghitung laju pemisahan.
Serta pada bidang geografi dan juga sosiologi: yang dipakai untuk menghitung laju pertumbuhan penduduk serta masih banyak lagi.
Aturan menentukan turunan fungsi
Turunan bisa kita tentukan tanpa adanya proses limit.Untuk kebutuhan ini dirancang teorema atau pernyataan mengenai turunan dasar, turunan dari operasi aljabar pada dua fungsi, aturan rantai untuk turunan fungsi komposisi, dan juga turunan fungsi invers.
Informasi selengkapnya simak pembahasan berikut ini:
Turunan dasar
Beberapa aturan dalam turunan fungsi antara lain:- f(x), menjadi f'(x) = 0
- Jika f(x) = x, maka f’(x) = 1
- Aturan pangkat berlaku jika f(x) = xn, maka f’(x) = n X n – 1
- Aturan kelipatan konstanta berlaku jika (kf) (x) = k. f’(x)
- Aturan rantai berlaku jika ( f o g ) (x) = f’ (g (x)). g’(x))
Turunan jumlah, selisih, hasil kali, serta hasil bagi dua fungsi
Contohnya fungsi f dan g terdiferensialkan pada selang I, maka fungsi f + g, f – g, fg, f/g, ( g (x) ≠ 0 pada I ) terdiferensialkan pada I dengan aturan sebagai berikut:- ( f + g )’ (x) = f’ (x) + g’ (x)
- ( f – g )’ (x) = f’ (x) – g’ (x)
- (fg)’ (x) = f’(x) g(x) + g’(x) f(x)
- ((f)/g )’ (x) = (g(x) f’ (x)- f(x) g’ (x))/((g(x)2)
Turunan fungsi trigonometri
- d/dx ( sin x ) = cos x
- d/dx ( cos x ) = – sin x
- d/dx ( tan x ) = sec2 x
- d/dx ( cot x ) = – csc2 x
- d/dx ( sec x ) = sec x tan x
- d/dx ( csc x ) = -csc x cot x
Turunan fungsi invers
(f-1)(y) = 1/(f’ (x)), atau dy/dx 1/(dx/dy)Rumus Dasar Turunan dari Turunan Fungsi
Beberapa aturan yang ada di dalam turunan fungsi antara lain:- f(x), menjadi f'(x) = 0
- Jika f(x) = x, maka f’(x) = 1
- Aturan pangkat berlaku jika f(x) = xn, maka f’(x) = n X n – 1
- Aturan kelipatan konstanta berlaku jika (kf) (x) = k. f’(x)
- Aturan rantai berlaku jika ( f o g ) (x) = f’ (g (x)). g’(x))
Sebab rumus ini akan kalian pakai untuk menyelesaikan persoalan dari turunan fungsi aljabar.
Rumus-rumus Turunan Fungsi Al Jabar
1. Rumus Turunan Fungsi PangkatTurunan Fungsi berbentuk pangkat, turunannya bisa memakai rumus:

Sehingga, rumus turunan fungsi pangkatnya adalah:
2. Rumus turunan hasil kali fungsi 
Rumusan Fungsi f(x) turunan yang terbentuk dari perkalian fungsi u(x) dan v(x), adalah sebagai berikut:
Sehingga, rumus turunan fungsinya yaitu:
f'(x) = u’v +uv’
3. Rumus turunan fungsi pembagian 

Sehingga, rumus turunan fungsinya yaitu:
4. Rumus turunan pangkat dari fungsi 
Perlu diingat, jika f(x) = xn , maka dari itu:
Sehingga, rumus turunan fungsinya yaitu:
f'(x) = nu(n – 1) . u’
5. Rumus-rumus Turunan Trigonometri
Berdasarkan definisi dari turunan, maka bisa kita dapatkan beberapa rumus turunan trigonometri yaitu sebagai berikut: (dengan u dan v masing-masing fungsi dari x), antara lain: y’ =- y = sin x→ y’ = cos x
- y = cos x → y’ = -sin x
- y = tan x → y’ = sec2 x
- y = cot x → y’ = -csc2 x
- y = sec x → y’
- y = csc x → y’ = csc × cot x
- y = sinn xy’ = n sinn-1 × cos x
- y = cosn x → y’ = -n cosn-1 × sin x
- y = sin u → y’ = u’ cos u
- y = cos u → y’ = u’ sin u
- y = tan u → y’ = ui sec2 u
- y = cot u → y’ = -u’ csc2 u
- y = sec u → y’ = u’ sec u tan u
- y = csc u → y’ = u’ csc u cot u
- y = sinn u → y’ = n.u’ sinn-1 cos u
- y = cosn u → y’ = -n.u’ cosn-1 . sin u
Turunan Fungsi Aljabar
Definisi Turunan
Turunan fungsi f(x) terhadap x didefinisikan oleh:Notasi Turunan
Turunan pertama fungsi y = f(x) pada x bisa kita notasikan seperti berikut ini:- y’ = f’x ⇒ lagrange
 ⇒ leibniz
⇒ leibniz- Dxy = Dx[f(x)]⇒ euler
- f(x) = k ⇒ f ‘(x) = 0
- f(x) = k x ⇒ f ‘(x) = k
- f(x) = xn ⇒ f ‘(x) = nxn-1
- f(x) = k u(x) ⇒ f ‘(x) = k u'(x)
- f(x) = u(x) ± v(x) ⇒ f ‘(x) = u'(x) ± v'(x)
dengan k = konstan
Perhatikan beberapa contoh berikut ini:
Untuk
mencari turunan dari fungsi yang memuat bentuk akar atau pecahan,
langkah pertama yang harus kita lakukan yaitu merubah terlebih dahulu
fungsi tersebut ke dalam bentuk pangkat (eksponen).Perhatikan beberapa contoh berikut ini:
- f(x) = 5 ⇒ f ‘(x) = 0
- f(x) = 2x ⇒ f ‘(x) = 2
- f(x) = x2 ⇒ f ‘(x) = 2x2-1 = 2x
- y = 2x4 ⇒ y’ = 2. 4x4-1 = 8x3
- y = 2x4 + x2 − 2x ⇒ y’ = 8x3 + 2x − 2
Berikut terdapat beberapa sifat akar dan pangkat yang sering dipakai, atara lain:
- xm . xn = xm+n
- xm/xn = xm-n
- 1/xn = x-n
- √x = x1/2
- n√xm = xm/n
Soal 1.
Tentukan turunan dari f(x) = x√x
Jawab:
f(x) = x√x = x. x1/2 = x3/2Soal 2.
f(x) = x3/2 →
Tentukan turunan dari
Jawab:
Turunan Perkalian dan Pembagian Dua Fungsi
Misalkan y = uv, maka turunan dari y bisa dinyatakan sebagai:
y’ = u’v + uv’
Misalkan y = u/v, maka turunan dari y dapat dinyatakan sebagai:
Contoh Soal.
Soal 1.
Turunan dari f(x) = (2x + 3)(x2 + 2) yaitu:
Jawab:
Misalkan:
u = 2x + 3 ⇒ u’ = 2
v = x2 + 2 ⇒ v’ = 2x
f ‘(x) = u’ v + u v’
f ‘(x) = 2(x2 + 2) + (2x + 3) 2x
f ‘(x) = 2x2 + 4 + 4x2 + 6x
f ‘(x) = 6x2 + 6x + 4
Aturan Rantai
Apabila y = f(u), dengan u merupakan fungsi yang bisa diturunkan pada x, maka turunan y terhadap x bisa dinyatakan dalam bentuk:
Dari konsep aturan rantai di atas, maka untuk y = un, akan didapatkan:

Secara umum bisa dinyatakan seperti berikut ini:
Apabila f(x) = [u(x)]n dengan u(x) merupakan fungsi yang bisa diturunkan pada x, maka:
f'(x) = n[u(x)]n-1 . u'(x)
Contoh Soal.Soal 1.
Tentukan turunan dari f(x) = (2x + 1)4
Jawab:
Misalnya:
u(x) = 2x + 1 ⇒ u'(x) = 2Soal 2.
n = 4
f ‘(x) = n[u(x)]n-1 . u'(x)
f ‘(x) = 4(2x + 1)4-1 . 2
f ‘(x) = 8(2x + 1)3
Tentukan turunan dari y = (x2 − 3x)7
Jawab :
y’ = 7(x2 − 3x)7-1 . (2x − 3)
y’ = (14x − 21) . (x2 − 3x)6
Latihan Soal & Pembahasannnya
Soal 1.Tentukanlah turunan fungsi dari f(x) = 2x(x4 – 5).
Jawab:
Misalkan jika u(x) = 2x dan v(x) = x4 – 5, maka:
u‘ (x) = 2 dan v‘ (x) maka = 4x3Dengan begitu, akan didapatkan penjabaran serta hasilnya:
f ‘(x) = u ‘(x).v(x) + u(x).v ’(x) = 2(x4 – 5) + 2x(4x3 ) = 2x4 – 10 + 8x4 = 10x4 – 10Soal 2. Soal Turunan Fungsi Aljabar
Turunan fungsi pertama dari
Jawab:
Soal ini merupakan soal fungsi yang berbentuk y = aun yang dapat dibahas dan diselesaikan dengan menggunakan rumus y’ = n . a . un-1. Maka:
Sehingga turunannya adalah:
Soal 3. Turunan Fungsi Trigonometri
Tentukan turunan pertama dari:
Jawab:
Untuk menyelesaikan perosalan di atas, kita bisa memanfaatkan rumus campuran yakni:
Sehingga:
serta juga bisa menggunakan rumus y’ = n. u’ sinn-1 u . cos u
Soal 4.
Turunan dari f(x) = (x – 1)2(2x + 3) adalah…
Jawab:
Misalkan:
u = (x − 1)2 ⇒ u’ = 2x − 2Soal 5.
v = 2x + 3 ⇒ v’ = 2
f ‘(x) = u’v + uv’
f ‘(x) = (2x − 2)(2x + 3) + (x − 1)2. 2
f ‘(x) = 4x2 + 2x − 6 + 2(x2 − 2x + 1)
f ‘(x) = 4x2 + 2x − 6 + 2x2 − 4x + 2
f ‘(x) = 6x2 − 2x − 4
f ‘(x) = (x − 1)(6x + 4) atau
f ‘(x) = (2x − 2)(3x + 2)
Apabila f(x) = x² – (1/x) + 1, maka f'(x) = . . . .
A. x – x²Jawab:
B. x + x²
C. 2x – x-2 + 1
D. 2x – x2 – 1
E. 2x + x-2
f(x) = x2 – (1/x) + 1
= x2 – x-1 + 1f'(x) = 2x -(-1)x-1-1
= 2x + x-2



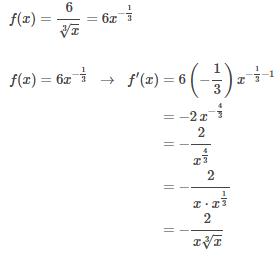



Komentar
Posting Komentar